あれ、なんでこんなに違うの? 直感の確率と客観的な確率 その2
こんにちは!ふくカエルです(Twitterアカウント:ふくカエル)。
ご訪問いただきましてありがとうございます!
今回は、クリティカルシンキング入門篇「あなたの思考をガイドする40の原則」を勉強してみます。
この記事は、あくまでもわたしの個人的な解釈に基づくものです。 中には、「これ違うんじゃないの?」という箇所もあるかと思います。 そのような場合は、温かい目でお見逃しくださいますよう、よろしくお願いします。
もっと、きちんと くわしく理解したいぞ~~~!
という方には、下記の書籍をご覧いただけるとありがたいです。
今回は、第5章「信念を分析する」からとなります。
前回の話
前回は、利用可能性ヒューリスティックスを使って感じる確率と、
客観的な確率とかなりズレることがあることをお知らせしました。
今回は
今回は、代表性ヒューリスティックスを使って確率を考えると、
これまた客観的な確率とはかなりズレる!
ことについてお知らせします。
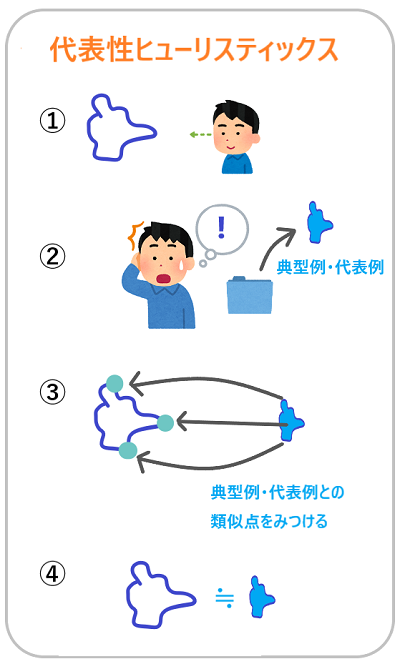
代表性ヒューリスティックスとは、
目の前の出来事が起こりやすいのかどうかの確率を判断するときに

自分の知識や情報によって、カテゴリされた典型例や代表例に、
どれだけ目の前の出来事が類似しているのか見つけて、

類似点があるほど確率が高いと主観的に考える方法です。

 ふくカエル
ふくカエル
 あれ、直感が当たらない? そんなときの直感の修正のしかたはこれ!
あれ、直感が当たらない? そんなときの直感の修正のしかたはこれ!
 ふくカエル
ふくカエル
この方法にも落とし穴があって、「感じる確率」が「歪んだ確率」になることがあります。
その前に考えて欲しいことがあります!
その前に、ちょっと考えて欲しいのです!
なぜ、確率をズレちゃうのか?
の理由を考える前に、
ちょっと考えて欲しいことがあります。

それは、次の問題です。
コインをランダムに投げたら、次のような順番で表裏が出ました。

- 表を〇
- 裏を✖
とすると、
実際に裏表が出た順番は、次のうちどちらの可能性が高いですか?
- 〇 ✖ 〇 ✖ 〇 ✖ 〇 ✖
- ✖ 〇 ✖ ✖ 〇 ✖ 〇 〇
答えは、1でも2でもあります。
つまり、どちらも同じです。
両者とも同じ確率2分の1の8乗になります。
こんな人いませんか?
「2」じゃね? と思った人いませんか?
と思った人いませんか?
感覚的に直観で「2」じゃないかな?
と思う人がいます。
「2」のほうがランダムに表裏が出ているような感じがするからです。
でも、どうしてこう「直観で感覚的な確率」と「客観的な確率」がズレちゃうのでしょうか?
なぜ、直観は、客観的な確率とズレちゃうのかな?
代表性ヒューリスティックスを使っちゃったから
まず、代表性ヒューリスティックスの方法を間違って使ったからです。
どうしても、コインをランダムに投げることから、
ランダムとは「規則正しく順番にでるもんじゃない」という典型例・代表例を引き出しちゃうのです。
そして、問題の選択肢から「1」を消去しちゃったのです。
ランダムな典型例に合わない
「設問」は消去だ!

と思ちゃうのです。
具体的にはこう!
「コインをランダム(偶然)に投げると、順番がバラバラになって出てくる!」
という典型例・代表例を自分の中から引っぱり出します。

次に、自分の典型例・代表例と「答えの選択肢」に類似点がないかを調べます。

「ランダム(偶然)ではない確率が高いだろう?」と思っちゃうのです。
「ランダム(偶然)である確率が高い!」と思ちゃうのです。
もっともこのような判断を、
脳みそは瞬時にサクサクと処理しているのは言うまでもないです。
実は、この問題で分かることがあるよ!
思考の癖も明らかになる!
実はです。
この問題をどのように考えたのかによって、「思考の癖」が明らかになってきます。
それは、
「小数の法則」への信念があるかどうか?
小数の法則とは、
- 長い時間
- 多くの試行
に当てはまる法則(これを大数の法則といいます)が
- 短い時間
- 少ない試行
でも当てはあると考えてしまう思考の癖のこといいます。
たとえば、サイコロの場合
たとえばサイコロの確率です。

サイコロの目の1から6までの目が出る確率は、
それぞれ6分の1です。
サイコロを何百回も投げれば、だんだんと「6分の1」に近づいてきて,
「ほぼ6分の1」になり落ち着きます(これを「大数の法則」といいます)。
何百回も投げるって
うんざりするよね!
 爪が剥がれそう・・・
爪が剥がれそう・・・
たしかに・・・
たしかに、
いくらそれぞれの目が出る確率が「6分の1」だからといっても、
サイコロを6回投げたら、常に必ずそれぞれの目が一つずつ出るとは限りません。
6回投げて、
それぞれの目が
必ず出るなんてあり得へん!
なので、試行回数がすくないときも、「大数の法則(徐々に6分の1に近づく)」が当てはまると考えるのです。
 ふくカエル
ふくカエル
 ふくネコ
ふくネコ
でもです。
コインの場合

でもです。
コインの裏表の出る確率のように「2分の1」の場合だと、ちっと事情が変わってきます。
サイコロの「6分の1」の場合と同じように考えちゃう(小数の法則を信じる)と
ちょっとズレてきます。
 ふくカエル
ふくカエル
錯覚してしまう
つまり、コインの裏表が
「裏」「表」「裏」「表」と交互に出てくることは、そうそうないことであり、
「これは偶然だ!」と思ってしまうのです。
実はこれ勘違いしてます。
「小数の法則の妖怪」にハマっているのです。
わしが、
小数の法則の妖怪じゃよ~。 小数の法則に、呪縛されとるよ!
小数の法則に、呪縛されとるよ!
よく考えると・・・
実は、落ち着いてよく考えると、
「2分の1」の確率なら規則正しく交互に出てくることって、普通にあります。
 ふくネコ
ふくネコ
そこで必要になる、クリティカルな思考になる第36の原則
大数において作用する法則を、小数の場合に単純にあてはめてはならない。
クリティカルシンキングより引用
こんな風にアレンジしてみた!
第36の原則
確率を考えるときに、
大数の法則が、
試行回数が少ない場合にも、すべてに当てはまると考えちゃダメだよ。
すべてに当てはまると考えちゃうと、
普通に起こる確率でも
「偶然だ!・ミラクルだ!」と大騒ぎすることになるよ。
後で、ちょっぴり恥ずかくなるよっ!
試行回数が
少ないときは要注意だよ!
まとめてみたkerokero
- 確率と代表性ヒューリスティックスについてお知らせしました。
- 代表性ヒューリスティックスを使うと自分が感じる確率と客観的な確率にズレが出てきます。
- 大数の法則を試行回数が少ないときにも当てはめようとする「少数法則への信念」には、注意したほうがいいです。
次回は、
「ギャンブラー錯誤」と、
 ふくカエル
ふくカエル
 ふくネコ
ふくネコ
「23人の誕生日の謎」についてお知らせします。

最後まで、読んでくださってありがとうございます。
またのお越しをお待ちしております。
ふくカエルでした。
なお、クリティカルシンキングの引用文は、宮元博章さん他お三方の日本語訳によりました。



