直観で感じる確率が客観的な確率とズレる場合! その3
こんにちは!ふくカエルです(Twitterアカウント:ふくカエル)。
ご訪問いただきましてありがとうございます!
今回は、クリティカルシンキング入門篇「あなたの思考をガイドする40の原則」を勉強してみます。
もっと、きちんと くわしく理解したいぞ~~~!
という方には、下記の書籍をご覧いただけるとありがたいです。
今回は、第5章「信念を分析する」からとなります。
前回の話
代表性ヒューリスティックスを使って確率を考えると、
これまた客観的な確率とはかなりズレる!
ことについてお知らせしました。
その中でも「小数の法則への信念」についてお知らせしました。
 あれ、なんでこんなに違うの? 直感の確率と客観的な確率 その2
あれ、なんでこんなに違うの? 直感の確率と客観的な確率 その2
今回は・・・
今回は、「ギャンブラー錯誤」と「23人の誕生日のパラドックス」についてお知らせします。
その前に考えて欲しいことがあります!
その前に、ちょっと考えて欲しいのです!
なぜ、直観だと確率を間違えちゃうのか?
の理由を考える前に、
ちょっと考えて欲しいことがあります。

それは、次の問題です。

前提として、
ルーレットを回して玉が赤いポケットに入る確率は、「50%よりも少し低い確率」として設定されています。
今10回ルーレットを回したところ、全部黒に入りました。

このような状況で、
次に赤いポケットに入る確率は、次のうちどれですか?
- 50%よりも少し低い
- ちょうど50%
- 50%よりも少し高い
- 50%よりかなり高い
質問2の答えは、「1」です。
確率は変わりません。
常に「50%よりほんの少し低い」になります。
こんな人いませんか?
黒ばっかり出てるんやろ?
もうそろそろ赤ちゃうか? だから、「3」か「4」やで。
だから、「3」か「4」やで。
と思った人いませんか?
なぜ、直観は客観的な確率とズレちゃうのかな?
ギャンブラー錯誤をしたから

なぜ、直観は客観的な確率とズレてしまったかというと、ギャンブラー錯誤をしてしまったからです。
ギャンブラー錯誤とは、
今まで起きた出来事の「偏り」を、次の出来事が修正すると勝手に考えることです。
たとえば、負けがこんでくると「次こそは勝つはずだ!」と根拠のない期待をしちゃうことです。
ギャンブルにありがちなことです。
めっちゃ大損したから
次は大儲けや! な~んて思っちゃう。
な~んて思っちゃう。
実は、この「ギャンブラー錯誤」も「小数の法則への信念」の一種です。
小数の法則について
 あれ、なんでこんなに違うの? 直感の確率と客観的な確率 その2
あれ、なんでこんなに違うの? 直感の確率と客観的な確率 その2
つまり、こんな風に考えちゃう
つまり、こんな風に考えてしまうのです。
10回もルーレットを回したのに、全部「黒」に入っているのなら、
近々「揺り戻し」が起こるぞ!
大まかな確率である「2分の1」に戻る確率が高い!
だから、次は「赤」に入る確率が高いに違いない!
と思ってしまうのです。
 ふくカエル
ふくカエル
でもです。
なんぼなんでも・・・
 ふくカエル
ふくカエル
なんぼなんでも、ルーレットが人間のように意志を持つわけないです。
 ふくネコ
ふくネコ
あれ~!10回も黒を出してもた~!
赤の確率50%切っとるやん!
あかんわ、次は赤を出しとこか!
な~んて、ルーレットが反省して、自分で修正するなんてありえないです。
 ふくカエル
ふくカエル
つまるところ・・・
つまりです。代表性ヒューリスティクスは、サンプルの数がいっぱいあるときは有効でも、
サンプルの数が少ないときは、当てはまらないことが増えてくるという欠点があるのです。
代表性ヒューリスティックスについて
 あれ、直感が当たらない? そんなときの直感の修正のしかたはこれ!
あれ、直感が当たらない? そんなときの直感の修正のしかたはこれ!
代表性ヒューリスティクスとは、簡単にいうと「自分の頭に浮かびやすい代表的な例と似たものを選びやすい」ということです。
- 「一度あることは二度ある」とか
- 「三度目の正直」とか
などのことわざは、
代表性ヒューリスティクスの典型例・代表例になります。
そこで必要になる、クリティカルな思考になる第37の原則
自然が自己修正を行なうという誤った信念(ギャンブラー錯誤)に惑わせれるな。
クリティカルシンキングより引用
こんな風にアレンジしてみた!
第37の原則
「自然」がこちらの都合の良いように、
確率を軌道修正なんかしないよ。
負けているときは、
藁でもすがりたいものさ! そんな弱さが期待として
そんな弱さが期待として
出ちゃうもんさ。
ここで、ちょっと考えてみませんか?
こんな場合はどう考えます?
ここでクエスチョンです!
ある部屋に23人の人がいます。
その中に同じ誕生日の人がいる確率はどれぐらいだと思いますか?
- 100分の1
- 10分の1
- 2分の1よりも大きい
答えはですね「3」です。
この問題は「誕生日のパラドックス」と言います。
えっつ!
50%ってか?
っんなもん!ありえへんわ~!
 間違ってるちゃう?
間違ってるちゃう?
と思った人たくさんいると思います。
 ふくカエル
ふくカエル
このパラドックスを理解すると、私たちの直観的な確率判断が、
いかに脆弱かがわかります。
 ふくカエル
ふくカエル
むずかしい計算はこちらの方を参考にしてください。
【答えの解説】
同じ誕生日である確率は、「同じ誕生日でない確率」を考えて、1から引き算すると出てきます。
まず、1人目の誕生日は365日のうちどの日付でもいいので、
同じ誕生日でない確率は
365/365=1
1人しかいない部屋に同じ誕生日の人がいるはずがないので、
同じ誕生日の人がいない確率は100%です。
次に、2人目の誕生日は、1人目の誕生日と違う日になるので、
365通りのうち、1人目を誕生日を除いた364通りあることになります。
同じ誕生日でない確率は
365/365×364/365=0.9973・・・
2人しかいない部屋に、
同じ誕生日でない確率は、99.7%になります。
また、3人目の誕生日は、1人目と2人目の誕生日と違う日になるので、
365通りのうち、1人目と2人目の誕生日を引いた363通りあることになります。
同じ誕生日でない確率は
365/365×364/365×363/365=09918・・・
3人しかない部屋に、
同じ誕生日でない確率は、99.1%になります。
以下、同じように4人目、5人目・・・と23人目まで計算していきます。
次のようになります。
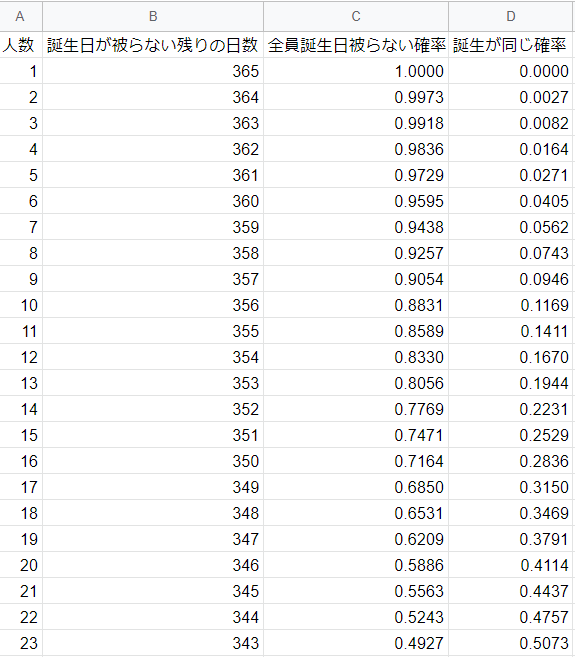
するとですね。
なっつなんと!
23人目のときは、
同じ誕生日でない確率は49.2%になるんです。
逆に言うと、同じ誕生日である確率は、50.7%になるんです。
1-0.4927=0.5073
すごいですね!
それでも、
納得できひんねんけど・・・
と思っている方に・・・
【こんな解説はどうでしょうか?】
23人の間に、
2人ペアの組み合わせが何通りあるのかを考えると納得できるかもしれません。
 ふくカエル
ふくカエル
つまり、23人中、2人ペアの組み合わせは、253通りあります。
計算式はこれね!
23(人分)×22(通りのペア)÷2=253通り
- 「1と2」のペア
- 「2と1」のペア
などの重複は除外するので、2で割ります。
253通りの組み合わせがあるので、その中で誕生日が同じであることもおかしいことじゃなくなります。
図解するとこんな感じです。
何を隠そう、前の職場ですごく相性の悪い人と誕生日が同じだったことがあります。
何か知らんけど
すごくショックでした。
実際に計算すると「さもありなん!」です。
まとめてみたkerokero
- 確率と代表性ヒューリスティックスについてお知らせしました。
- 代表性ヒューリスティックスを使うと自分が感じる確率と客観的な確率にズレが出てきます。
- 「ギャンブラー錯誤」には注意したほうがいいです。
- 直観を裏切る「23人の誕生日」は覚えておくと役立ちます。
次回は、「ネジ巻の時計の謎」とについてお知らせします。
最後まで、読んでくださってありがとうございます。
またのお越しをお待ちしております。
ふくカエルでした。
なお、クリティカルシンキングの引用文は、宮元博章さん他お三方の日本語訳によりました。



