原因をちゃんと特定する方法 その３
こんにちは！ふくカエルです（Twitterアカウント：ふくカエル）。
ご訪問いただきましてありがとうございます！
今回は、クリティカルシンキング入門篇「あなたの思考をガイドする４０の原則」を勉強してみます。
もっと、きちんと くわしく理解したいぞ～～～！
という方には、下記の書籍をご覧いただけるとありがたいです。
前回のお話
前前々回のお話は、
人はものごとの原因を探るときに、とかく自分の目がつきやすいものを
これが、原因に違いない！
と「安易に決めつけちゃう傾向があるので問題だよね」
ということをお話しました。
こんな風に原因を考えちゃいませんか？ 気をつけたい落とし穴について。
決めつけや、思い込みで
大失敗しちゃうかもしれん！
そこで、
ふくカエル
ということで、
因果関係の有無の判断の方法を考えたのが前々回と前回です。
ふくカエル
今回は、「③もっともらしい他の原因の排除」について考えてみます。
もっともらしい他の原因の排除とは、何かな？
う～ん。ムズイ！
この因果関係の有無を判断する基準は、もっともクリティカルな思考が必要となります。
そして、ムズイ（むずかしい）のです。
この「もっとらしい他の原因」という日本語からして、変な言い回しでむずかしいです。
ムズムズする！
でも、頑張るねん！
もっともらしい他の原因の排除とは？
もっともらしい他の原因の排除とは、
ひょっとして、
出来事Ⅹが出来事Ｙの原因じゃないか？
と考えられるときに、
「これが原因だ！」と正しく判断するために、
出来事Ｘ以外に原因になりそうなその他の出来事を探してみます。
探してもなかった場合のみ、
出来事Ｘが正真正銘の原因だ！
と決め打っちゃってもＯＫだよ！っていう基準です。
こんなときに役立つ
このムズイ基準ですが、次のようなときに役立ちます。
たとえば、
出来事Ｘと出来事Ｙの間に「共変関係（共に変化する）」があるときに、
ふくカエル
目につく状況のみに注目して、出来事Ｘと出来事Ｙの間の因果関係があると安易に即断したり、
どう、即断する俺って！
あほか！
間違えとるぞ！
背後に本当の原因である別の出来事Ｚが隠れているのにスルーしてしまったり、
あっつ、しもた！
見逃がしたかもしれん！
するような危険な状況を回避するのに役立ちます。
「もっともらしい他の原因」を考えるときには、次の問題が参考になります。
たとえば、アイスクリームの問題
たとえば、「原因をちゃんと特定する方法 その１」で考えた問題です。
月別のアイスクリーム売り上げと犯罪発生率は関係あるのか？という問題でした。
たしかに、アイスクリームの売り上げが増えれば、犯罪発生率は増えるという「共感関係（ともに変化する）」があります。
でもです。
このときに誰も、
「アイスクリームが犯罪発生の直接の原因となる！」
とまでは考えなかったと思います。
ふくカエル
ふくネコ
アイス食べたら、
ドロボーしたくなっちゃう！
なんてことになると！
そら、吹くわな！
それに
アイスクリーム工場も
泣くわな。
でも、「気温の上昇が不快指数をあげる」という事情を介在すると、
アイスクリーム売り上げの増加と犯罪発生率の増加はつながります。
この「気温上昇」が背後に隠れていた「原因」になります。
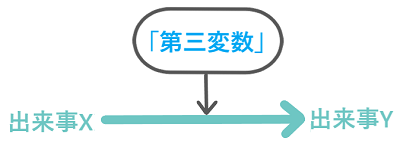
これを第三変数と言うよ！
「ほんまの原因」は僕やねん。
隠れとってん！
この背後に隠れていた「原因」を「第三変数」と言います。
「もっともらしい他の原因を考える」とは、この「第三変数」を考えることになります。
「もっともらしい原因を排除する」とは、この「第三変数の可能性」を排除することになります。
そこで必要になる、クリティカルな思考になる第７の原則
因果関係の根拠を求める際、
第三変数が存在する可能性を注意深くさぐれ。
クリティカルシンキングより引用
第７の原則
そこで、クリティカルな思考するために「第７の原則」が必要になってきます。
第７の原則
因果関係の有無の判断をするときには、
「第三変数」はないのか？
常に注意しよう！
この原則を常に頭に置いておくと、因果関係を有無を判断するときに楽になります。
共変関係があったとしても、因果関係が必ずしもあるとは限りません。
たとえ一見して、
この出来事があったらこの出来事がおきた！
と思えたとしても、
原因と結果に違いない！
って思わないように
しましょう！
そして、背後に隠れている「もっともらしい他の原因（第三変数）」をじっくりと探るようにしましょう！
ここで、ちょっと考えてみませんか？
次の出来事に「第三変数」があります。それは何でしょう？
どの設問も一見すると奇妙ですが、実は相関関係があります。
- その人の体重とその人のボキャブラリーの豊富さの間
- 自動車を持っている学生が起した交通事故・違反の回数とその学生の成績の平均点
- 小学校高学年の児童の国語のテストの点数と髪の毛の長さ
体重の重さとボキャブラリーの豊富さ
体重が重たい人ほど、ボキャブラリーが豊富になります。
一見奇妙な相関関係ですが、「第三変数」を介在すると、
誰もが納得できる相関関係になります！
うふふ。
この設問では、年齢の幅を設けず、全年齢の人々を対象にして考えるのがポイントです。
赤ちゃんと大人を考えると相関関係があるとわかります。
赤ちゃんは、大人に比べて体重も軽いし、ボキャブラリーも少ないです。
ここでの「第三変数」とは「年齢」です。
「年齢」という「第三変数」が隠されているので一見すると奇妙に思えるのです。
交通事故・違反の回数と成績の平均点
交通事故・違反の回数が多い学生ほど、成績の平均点が低くなります。
「第三変数」（介在するもっともらしい原因）は何でしょう？
この設問では、まじめさや品性を考えるのがポイントです。
成績が良い生徒ほど、まじめで落ち着きがあります。
また勉強する時間が長いほど、運転する暇がないことも上げられます。
「まじめさや品性」「勉強時間」という「第三変数」の可能性が隠されています。
国語のテストの点数と髪の毛の長さ
小学校高学年の児童に限って、国語の成績が良い児童ほど髪の毛が長いです。
最後の設問になります。「第三変数」（介在するもっともらしい原因）は何でしょう？
この設問では、性別を考えるのがポイントです。
小学校高学年の児童の年齢では、女児の方が語学的能力が優れていると考えられています。
女児は、男児にくらべて髪の毛が長いです。
ここでの「第三変数」は「性別」です。
まとめてみたkerokero
- 原因を特定する方法について、第７原則をお知らせしました。
- 原因を特定するためには、出来事と出来事の間に因果関係の有無を確認することが必要になります。
- 因果関係があると言えるためには、３つの基準が満たされる必要があります。
- 今回は３つ目の基準「もっともらしい他の原因を排除する」についてお知らせしました。
今回は、因果関係の第三の基準である「もっともらしい他の原因の排除」についてお知らせしました。
今回お知らせしていませんが、
本書には「喫煙は有害かどうか？」について興味深いことが書かれています。
次回は、お知らせした「三つの基準」以外に、
これは知っといたほうがいいよという原則をいくつかお知らせします。
最後まで、読んでくださってありがとうございます。
またのお越しをお待ちしております。
ふくカエルでした。
なお、クリティカルシンキングの引用文は、宮元博章さん他お三方の日本語訳によりました。